Лабораторная работа № 2-1

При движении частицы массы m и зарядом q, под действием только электрических сил от точки с потенциалом φ₁ до точки с потенциалом φ₂, кинетическая энергия частиц изменяется от до . По закону сохранения энергии имеем:

где qφ₁ и qφ₂ - потенциальные энергии частицы в точках с соответствующими потенциалами. Работа А сил электростатического поля в этом случае будет:

Объединив формулы (1-9) и (1-10) и учитывая, что , получим формулу связи напряженности и потенциала:

т.е. напряженность поля численно равна изменению потенциала dφ на единицу длины dr, отсчитанному в направлении, перпендикулярном к поверхности потенциала, и направлена в сторону убывания потенциала (знак минус).

Величина, указывающая быстроту изменения потенциала при перемещении в направлении, перпендикулярном к поверхности уровня потенциала, называется градиентом потенциала, т.е.

Геометрическое место точек электрического поля, потенциалы которых одинаковы, называется эквипотенциальной поверхностью или поверхностью равного потенциала, при перемещении заряда по эквипотенциальной поверхности изменение потенциала dφ равно нулю, поэтому работа сил электростатического поля при таком перемещении равна нулю, что говорит о перпендикулярности электростатических сил к направлению перемещения и, следовательно, перпендикулярности силовых линий и эквипотенциальных поверхностей.

Вектор напряженности данной точки электрического поля направлен по нормали к эквипотенциальной поверхности, проведенной через эту точку. На рис.3 изображено электрическое поле, образованное положительным точечным зарядом q и отрицательно заряженной плоскостью Р. Сплошные линии - эквипотенциальные поверхности с потенциалами φ₁, φ₂, φ₃ и т.д., пунктирные - силовые линии поля.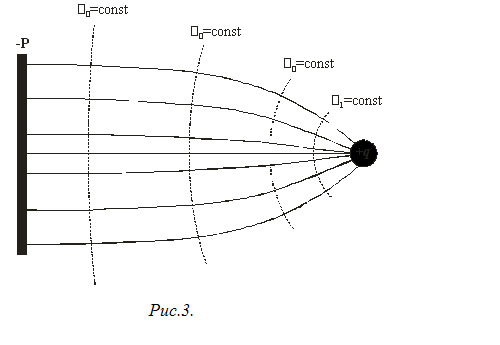

При движении электрического заряда q по замкнутой линии в электрическом поле, его начальная и конечная потенциальная энергии одинаковы. Следовательно, работа сил электрического поля при таком движении будет равна нулю:

т.к. , то

Выражение в левой части формулы (1-14) называется циркуляцией вектора напряженности (рис.4).

Интернет-магазин