Лабораторная работа № 2-4Б
Концентрация электронов в зоне проводимости будет равна

Из уравнения (4Б-3) видно, что концентрация электронов в зоне проводимости будет расти с повышением температуры. Разность E - μ можно считать равной половине ширины запрещенной зоны, т.е. 2(E-μ)=E_g. Тогда формула (4Б-3) примет вид:

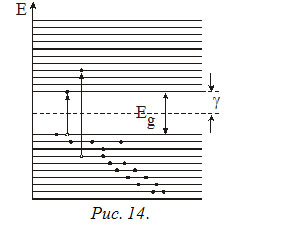
E_g называют также энергией активации, т.е. это энергия, которую необходимо сообщить электрону, чтобы перевести его из валентной зоны в зону проводимости. Энергия активации является важнейшей характеристикой электрических свойств полупроводника.
Подстановка (4Б-4) в (4Б-1) дает выражение:

Удельная электрическая проводимость полупроводника γ связана с плотностью тока законом Ома в дифференциальной форме

Здесь , ρ - удельное сопротивление, - напряженность электрического поля. Из выражения (4Б-5) и (4Б-6) найдем γ и, обозначая произведение всех постоянных для данного полупроводника величин , получим

Увеличение проводимости полупроводников с повышением температуры является их характерной особенностью. С точки зрения данной теории это обстоятельство объясняется так: с повышением температуры растет число электронов, которые вследствие теплового возбуждения переходят в зону проводимости и участвуют в проводимости.
В данной работе экспериментально определяется сопротивление R полупроводника, которое связано с γ формулой:

Подставляя (4Б-7) в (4Б-8), получим

где 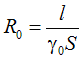- постоянная величина для данного полупроводника. Графиком зависимости сопротивления от температуры будет убывающая экспонента, как на рис.16а.
Для нахождения энергии активации E_g прологарифмируем выражение (4Б-9):

График зависимости (4Б-10) будет линейным с положительным угловым коэффициентом как на рис.16б. По наклону графика можно определить ширину запрещенной зоны:

где k - постоянная Больцмана (k 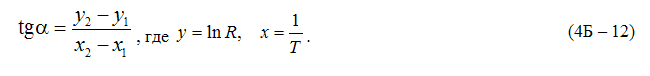1,38 10^-23 Дж/К). Тангенс угла наклона можно определить по двум точкам на графике:


Интернет-магазин