ЛАБОРАТОРНАЯ РАБОТА № 3–11
ИЗУЧЕНИЕ ДИФРАКЦИИ ФРЕНЕЛЯ НА КРУГЛОМ ОТВЕРСТИИ

Приборы и принадлежности: оптическая скамья, коллиматор с диафрагмой, светофильтр, окулярный микроскоп.

Цель работы: изучение дифракции Френеля на круглом отверстии.

1. Краткая теория

Пусть на пути плоской волны находится непрозрачный экран с отверстием (рис. 34). Построив, согласно принципу Гюйгенса, огибающую элементарных волн, мы заметим, что фронт волны входит в область геометрической тени, создаваемой экраном.

Световая волна огибает встречные непрозрачные тела, отклоняясь от прямолинейного распространения. Это явление называется дифракцией света.

Однако принцип Гюйгенса дает только качественную картину дифракции. Френель дополнил его следующим утверждением.

Пусть в некоторый момент времени фронт волны достиг положения ОО₁. Амплитуда колебаний в точке P, лежащей перед фронтом волны, является результатом интерференции элементарных волн, исходящих от каждого элемента волнового фронта dS.

Непосредственное применение принципа Гюйгенса-Френеля для интегрирования элементарных волн связано, как правило, с большими математическими трудностями. Френель предложил более простой приближенный метод, получивший название метода зон Френеля.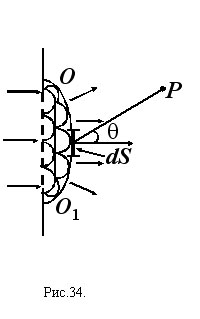

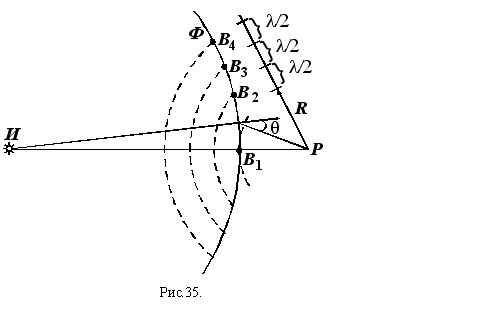
Пусть Ф – фронт волны, испускаемой точечным источником света И (рис. 35). Найдем интенсивность света в точке P по мере открывания фронта волны, начиная с точки В₁. Для этого выделим из фронта волны зоны Френеля, проводя сферы с центром в точке P и радиусами R=PB₁, R + λ / 2, R + 2λ / 2, R + 3λ / 2, …, и т.д. Определим А₁ – амплитуду колебаний в точке P, создаваемую действием одной только первой зоны. Для этого разделим зону на кольцевые участки одинаковой площади и очень малой ширины. Первый (точка B₁) и последний участки (кольцо на расстоянии R + λ / 2 от точки P) дадут колебания в точке P, сдвинутые по фазе на 180^o, а все промежуточные участки дадут колебания с непрерывно изменяющимися разностями фаз от 0 до 180^o. поэтому суммарная амплитуда колебаний в точке P должна соответствовать диаметру полуокружности, построенной как векторная сумма бесконечно малых векторов – амплитуд колебаний, приходящих от отдельных участков первой зоны (рис. 36а).