Откроем в дополнение к первой еще и вторую зону Френеля. Это означает, что при сложении элементарных амплитуд надо добавить еще одну полуокружность, чтобы вектор амплитуды колебаний от последнего участка 2-ой зоны (кольцо, проходящее через точку B₃) совпал по фазе с вектором от первого участка 1-ой зоны (точка B₁).

Если 1-ая и 2-ая зоны были одинаково расположены относительно точки P и их площади были одинаковы, то полуокружности замкнулись, образовав полную окружность, и сумма всех элементарных колебаний оказалась бы равной нулю.

На самом же деле, как это видно из рис. 35, расстояния от элементарных участков до точки P и углы θ возрастают, что приводит к постепенному убыванию элементарных амплитуд. Поэтому сложение элементарных амплитуд происходит не по окружности, а по спирали. Поэтому, в результате действия двух зон, получается отличная от нуля, но весьма малая амплитуда А₂ (рис. 36б). Открывая еще и третью зону, мы получим большую амплитуду (но несколько меньшую, чем А₁ (А₃, рис. 36в).

Таким образом, освещенность в точке P зависит от того, сколько зон Френеля будет открыто. Если открыто нечетное число зон Френеля, освещенность усиливается, а четное – ослабляется. Когда будет открыт весь фронт волны, мы получим амплитуду 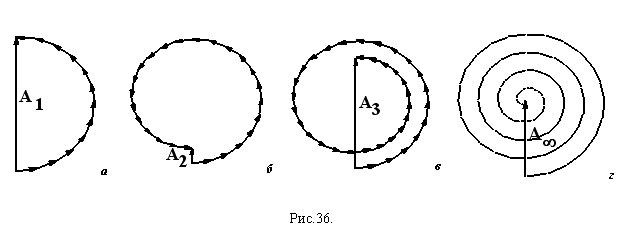. Из рисунка 36г видно, что .

Таким образом, установив в точке B₁ диаграмму и постепенно раскрывая ее, мы будем наблюдать последовательные усиления и ослабления освещенности в точке P в соответствии с диаграммой амплитуд, приведенной на рис. 36г. Причем, освещенность в отсутствии диаграммы будет такой же, когда открыта лишь половина 1-ой зоны Френеля.

Определим размеры этой зоны. Будем полагать, что фронт падающей волны плоский, для этого достаточно на оптической оси поставить линзу, совместив ее фокус с источником. В этом случае радиусы зон Френеля определяются так же, как и радиусы колец Ньютона [см. формулу (8-4) лабораторной работы 3-8], где n – номер зоны, R – расстояние от точки наблюдения до экрана, λ – длина волны. Пусть R = 1 м, λ = 5 • 10^–7 м, тогда для радиуса 1-ой зоны получим . Контролировать изменения столь малых диафрагм чрезвычайно трудно. Но опыт можно провести при постоянной диафрагме, изменяя расстояние R. Перемещая точку наблюдения, можно заметить на оптической оси изменения освещенности в соответствии с амплитудами А₁, А₂, А₃, …, когда в отверстии диафрагмы будут помещаться одна, две, три и т.д. зоны Френеля. Эти наблюдения и проводятся в данной работе.